جلسه دوم

الگو ها

تمرین ۱: خط ستاره

الگوی زیر را چاپ کنید:

*****

راهنمایی: از یک حلقه ساده استفاده کنید.

ورودی: عدد n (تعداد ستاره‌ها)

n = 5

خروجی:

*****

تمرین ۲: مثلث ساده

الگوی زیر را چاپ کنید:

*
**
***
****
*****

راهنمایی: از دو حلقه تو در تو استفاده کنید. حلقه بیرونی تعداد خطوط و حلقه درونی تعداد ستاره‌های هر خط را کنترل می‌کند.

ورودی: عدد n (تعداد سطرها)

n = 5

خروجی:

*
**
***
****
*****

تمرین ۳: جدول ضرب ۱۰×۱۰

با استفاده از \t جدول ضرب زیر را چاپ کنید:

1  2  3  4  5  6  7  8  9  10
2  4  6  8  10  12  14  16  18  20
3  6  9  12  15  18  21  24  27  30
...

راهنمایی: از دو حلقه تو در تو و عملگر ضرب استفاده کنید. برای فاصله‌گذاری مناسب از \t استفاده کنید.

ورودی: عدد n (ابعاد جدول)

n = 5

خروجی:

1  2  3  4  5
2  4  6  8  10
3  6  9  12  15
4  8  12  16  20
5  10  15  20  25

تمرین ۴: مثلث وارونه

الگوی زیر را چاپ کنید:

*****
****
***
**
*

راهنمایی: مشابه تمرین ۲، اما شروع حلقه را از عدد بزرگتر در نظر بگیرید.

ورودی: عدد n (تعداد سطرها)

n = 5

خروجی:

*****
****
***
**
*

تمرین ۵: هرم

الگوی زیر را چاپ کنید:

    *
   ***
  *****
 *******
*********

راهنمایی: به سه مورد دقت کنید: ۱. فضاهای خالی در ابتدای هر خط ۲. تعداد ستاره‌ها در هر خط (فرد است) ۳. رابطه بین شماره خط و تعداد ستاره‌ها

ورودی: عدد n (تعداد سطرها)

n = 5

خروجی:

    *
   ***
  *****
 *******
*********

تمرین ۶: مربع توخالی

الگوی زیر را چاپ کنید:

*****
*   *
*   *
*   *
*****

راهنمایی: شرط‌های خاص برای:

• خط اول و آخر
• ستون‌های کناری
• فضای خالی وسط در نظر بگیرید.

ورودی: عدد n (طول ضلع)

n = 5

خروجی:

*****
*   *
*   *
*   *
*****

تمرین ۷: لوزی

الگوی زیر را چاپ کنید:

  *
 ***
*****
 ***
  *

راهنمایی: ترکیبی از هرم و مثلث وارونه است.

ورودی: عدد n (نصف ارتفاع + 1)

n = 3

خروجی:

  *
 ***
*****
 ***
  *

نکات مهم برای همه تمرین‌ها

۱. قبل از شروع کدنویسی، الگو را تحلیل کنید ۲. تعداد تکرار حلقه‌ها را مشخص کنید ۳. برای هر الگو، ابتدا با مقادیر کوچک تست کنید ۴. از متغیر ورودی n برای تعیین اندازه الگو استفاده کنید

چالش‌های اضافی

۱. برنامه‌ها را طوری بنویسید که اندازه الگو را از کاربر دریافت کنند ۲. جدول ضرب را طوری تغییر دهید که اعداد تک رقمی با یک فاصله اضافه نمایش داده شوند ۳. سعی کنید هرم را به صورت متقارن (با تعداد ستاره‌های زوج) چاپ کنید ۴. الگوهای جدید طراحی کنید

راه‌حل‌های نمونه

پاسخ‌های پیشنهادی

# تمرین ۱: خط ستاره
def pattern1(n):
    print('*' * n)

# تمرین ۲: مثلث ساده
def pattern2(n):
    for i in range(1, n+1):
        print('*' * i)

# تمرین ۳: جدول ضرب
def pattern3(n):
    for i in range(1, n+1):
        for j in range(1, n+1):
            print(i*j, end='\t')
        print()

# تمرین ۴: مثلث وارونه
def pattern4(n):
    for i in range(n, 0, -1):
        print('*' * i)

# تمرین ۵: هرم
def pattern5(n):
    for i in range(n):
        print(' ' * (n-i-1) + '*' * (2*i+1))

# تمرین ۶: مربع توخالی
def pattern6(n):
    for i in range(n):
        if i == 0 or i == n-1:
            print('*' * n)
        else:
            print('*' + ' ' * (n-2) + '*')

# تمرین ۷: لوزی
def pattern7(n):
    # بالای لوزی
    for i in range(n):
        print(' ' * (n-i-1) + '*' * (2*i+1))
    # پایین لوزی
    for i in range(n-2, -1, -1):
        print(' ' * (n-i-1) + '*' * (2*i+1))

# نمونه اجرا
if __name__ == '__main__':
    n = int(input('Enter n: '))
    pattern1(n)

دوره هفته گذشته + حل آنها با

مسئله ۱: شمارش ارقام (Digit Counter)

یک عدد صحیح را دریافت کرده و تعداد ارقام آن را برگردانید.

ورودی نمونه:

23415

خروجی نمونه:

5

مسئله ۲: مجموع اعداد زوج (Sum of Even Digits)

یک عدد صحیح را دریافت کرده و مجموع ارقام زوج آن را محاسبه کنید.

ورودی نمونه:

23415

خروجی نمونه:

6 # (2 + 4)

راهنمایی

برای جدا کردن ارقام یک عدد می‌توانید از عملیات‌های تقسیم (/) و باقیمانده (%) استفاده کنید.

ماژول به 10 یکان عدد را به ما میدهد. yekan = a%10 همچنین تقسیم عدد به ده در واقع یک رقم از سمت راست حذف میکند.

با این فرمول مثلا اگر رقم صدگان یک عدد را بخواهیم ابتدا باید آنرا تقسیم به صد کنیم بعد ماژول به ده بگیریم

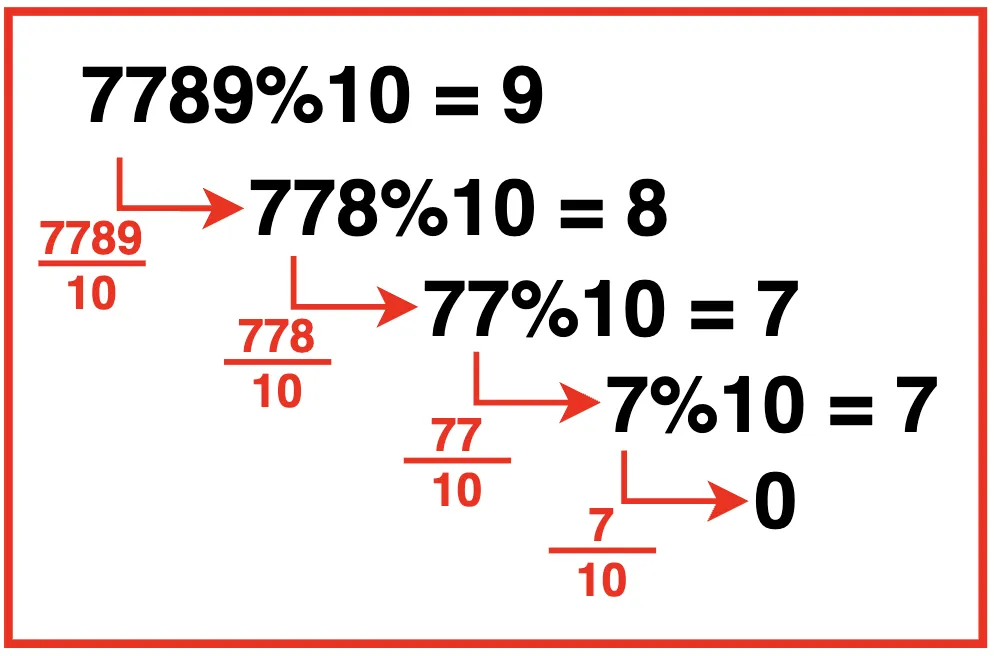
مسئله ۳: بزرگترین رقم (Maximum Digit)

یک عدد صحیح را دریافت کرده و بزرگترین رقم آن را برگردانید.

ورودی نمونه:

23415

خروجی نمونه:

5

مسئله ۴: آینه‌ای بودن (Is Palindrome)

تعیین کنید آیا یک عدد آینه‌ای است یا خیر.

ورودی نمونه:

12321

خروجی نمونه:

True

جواب

مشابه سوال جمع ارقامه. فقط اینور یه متغیر تعریف میکنیم و هر رقمی که جدا کردیم توی این متغیر اضافه میکنیم با توجه به ارزش مکانیش. البته چون این یه حلقه است پس فقط کافیه در ده ضرب کنیم

حل مسائل دوره

راه حل‌ها (Solutions)

حل ۱: شمارش ارقام

# Recursive Solution
def count_digits_recursive(n):
    if n < 10:
        return 1
    return 1 + count_digits_recursive(n // 10)

# Iterative Solution
def count_digits_iterative(n):
    count = 0
    while n > 0:
        count += 1
        n //= 10
    return count

حل ۲: مجموع اعداد زوج

# Recursive Solution
def sum_even_digits_recursive(n):
    if n == 0:
        return 0
    digit = n % 10
    if digit % 2 == 0:
        return digit + sum_even_digits_recursive(n // 10)
    return sum_even_digits_recursive(n // 10)

# Iterative Solution
def sum_even_digits_iterative(n):
    total = 0
    while n > 0:
        digit = n % 10
        if digit % 2 == 0:
            total += digit
        n //= 10
    return total

حل ۳: بزرگترین رقم

# Recursive Solution
def max_digit_recursive(n):
    if n < 10:
        return n
    return max(n % 10, max_digit_recursive(n // 10))

# Iterative Solution
def max_digit_iterative(n):
    max_digit = 0
    while n > 0:
        max_digit = max(max_digit, n % 10)
        n //= 10
    return max_digit

حل ۴: آینه‌ای بودن

# Recursive Solution
def is_palindrome_recursive(n):
    # Helper function to get number length
    def get_length(num):
        if num < 10:
            return 1
        return 1 + get_length(num // 10)

    # Helper function to get digit at position
    def get_digit(num, pos):
        return (num // (10 ** pos)) % 10

    def check_palindrome(num, start, end):
        if start >= end:
            return True
        if get_digit(num, start) != get_digit(num, end):
            return False
        return check_palindrome(num, start + 1, end - 1)

    length = get_length(n)
    return check_palindrome(n, 0, length - 1)

# Iterative Solution
def is_palindrome_iterative(n):
    original = n
    reversed_num = 0
    while n > 0:
        reversed_num = reversed_num * 10 + n % 10
        n //= 10
    return original == reversed_num

مسائل پیشرفته تر

۱. پرانتزهای معتبر (سطح: آسان)

تعیین کنید آیا یک رشته از پرانتزها معتبر است یا خیر.

قوانین اعتبارسنجی:

1. پرانتزهای باز باید با همان نوع پرانتز بسته شوند
2. پرانتزهای باز باید به ترتیب درست بسته شوند
3. هر پرانتز بسته باید یک پرانتز باز متناظر از همان نوع داشته باشد

نمونه ورودی/خروجی:

ورودی ۱: s = "()"
خروجی ۱: true

ورودی ۲: s = "()[]{}"
خروجی ۲: true

ورودی ۳: s = "(]"
خروجی ۳: false

ورودی ۴: s = "([])"
خروجی ۴: true

محدودیت‌ها:

• 1 <= s.length <= 10^4
• s فقط شامل پرانتزها '()[]{}' است

۲. پیشوند مشترک طولانی‌ترین (سطح: آسان)

طولانی‌ترین پیشوند مشترک بین مجموعه‌ای از رشته‌ها را پیدا کنید.

نمونه ورودی/خروجی:

ورودی ۱: strs = ["flower", "flow", "flight"]
خروجی ۱: "fl"

ورودی ۲: strs = ["dog", "racecar", "car"]
خروجی ۲: ""
توضیح: هیچ پیشوند مشترکی بین رشته‌های ورودی وجود ندارد.

محدودیت‌ها:

• 1 <= strs.length <= 200
• 0 <= strs[i].length <= 200
• رشته‌ها فقط شامل حروف کوچک انگلیسی هستند

۳. ماندگاری ضربی (سطح: متوسط)

ماندگاری ضربی یک عدد، تعداد دفعاتی است که باید ارقام آن را در هم ضرب کنیم تا به یک رقم برسیم.

مثال محاسبه:

39 => 3*9 = 27 => 2*7 = 14 => 1*4 = 4
پاسخ: 3 (سه مرحله طول کشید)

نمونه ورودی/خروجی:

ورودی ۱: 999
خروجی ۱: 4

ورودی ۲: 5355
خروجی ۲: 3

محدودیت‌ها:

• 0 <= N <= 100000
• فقط راه‌حل بازگشتی قابل قبول است

۴. کامل بودن یا نبودن (سطح: متوسط)

تعیین کنید آیا یک عدد کامل است یا خیر. عددی کامل است اگر مجموع مقسوم‌علیه‌های آن (به جز خودش) برابر با خود عدد باشد.

نمونه ورودی/خروجی:

ورودی ۱: 27
خروجی ۱: NO
توضیح: مقسوم‌علیه‌ها: 1 + 3 + 9 = 13 ≠ 27

ورودی ۲: 6
خروجی ۲: YES
توضیح: مقسوم‌علیه‌ها: 1 + 2 + 3 = 6

محدودیت‌ها:

• 2 <= n <= 200000

۵. سودوکو معتبر (سطح: متوسط)

تعیین کنید آیا یک جدول سودوکو ۹×۹ معتبر است یا خیر.

قوانین اعتبارسنجی:

1. هر سطر باید شامل ارقام ۱-۹ بدون تکرار باشد
2. هر ستون باید شامل ارقام ۱-۹ بدون تکرار باشد
3. هر بلوک ۳×۳ باید شامل ارقام ۱-۹ بدون تکرار باشد

نکته: فقط خانه‌های پر شده نیاز به بررسی دارند.

نمونه ورودی/خروجی:

ورودی ۱:
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
خروجی ۱: true

محدودیت‌ها:

• board.length == 9
• board[i].length == 9
• اعداد موجود بین ۱-۹ یا ’.’ هستند

۶. چرخش آرایه (سطح: متوسط)

یک آرایه عددی را به اندازه k گام به راست بچرخانید.

نمونه ورودی/خروجی:

ورودی ۱: nums = [1,2,3,4,5,6,7], k = 3
خروجی ۱: [5,6,7,1,2,3,4]

ورودی ۲: nums = [-1,-100,3,99], k = 2
خروجی ۲: [3,99,-1,-100]

محدودیت‌ها:

• 1 <= nums.length <= 10^5
• -2^31 <= nums[i] <= 2^31 - 1
• 0 <= k <= 10^5

۷. دزد خانه (سطح: اصلا هم درد نداشت)

برنامه‌ای بنویسید که حداکثر مقدار پولی را که می‌توان از خانه‌های غیرمجاور دزدید محاسبه کند.

نمونه ورودی/خروجی:

ورودی ۱: nums = [1,2,3,1]
خروجی ۱: 4
توضیح: خانه‌های ۱ و ۳ را بدزدید (1 + 3 = 4)

ورودی ۲: nums = [2,7,9,3,1]
خروجی ۲: 12
توضیح: خانه‌های ۱، ۳ و ۵ را بدزدید (2 + 9 + 1 = 12)

محدودیت‌ها:

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400

۷. تعداد جزیره‌ها (سطح: یکم سخت)

در یک نقشه دودویی، تعداد جزیره‌ها را بشمارید. جزیره با ‘1’ نشان داده می‌شود و آب با ‘0’.

نمونه ورودی/خروجی:

ورودی ۱:
[
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
خروجی ۱: 1

ورودی ۲:
[
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
خروجی ۲: 3

محدودیت‌ها:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] is '0' یا '1'

۸. عدد جمع‌پذیر (سطح: متوسط)

تعیین کنید آیا یک رشته عددی می‌تواند یک دنباله جمع‌پذیر تشکیل دهد یا خیر.

نکته: اعداد نمی‌توانند با صفر شروع شوند.

نمونه ورودی/خروجی:

ورودی ۱: "112358"
خروجی ۱: true
توضیح: 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8

ورودی ۲: "199100199"
خروجی ۲: true
توضیح: 1 + 99 = 100, 99 + 100 = 199

محدودیت‌ها:

• 1 <= num.length <= 35
• num فقط شامل ارقام است

۹. دزد خانه (سطح: اصلا هم درد نداشت)

برنامه‌ای بنویسید که حداکثر مقدار پولی را که می‌توان از خانه‌های غیرمجاور دزدید محاسبه کند.

نمونه ورودی/خروجی:

ورودی ۱: nums = [1,2,3,1]
خروجی ۱: 4
توضیح: خانه‌های ۱ و ۳ را بدزدید (1 + 3 = 4)

ورودی ۲: nums = [2,7,9,3,1]
خروجی ۲: 12
توضیح: خانه‌های ۱، ۳ و ۵ را بدزدید (2 + 9 + 1 = 12)

محدودیت‌ها:

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400